RESEARCH ARTICLE
A Physiological Dynamic Testing Machine for the Elbow Joint
Johannes Kiene 1, Robert Wendlandt 2, Marcus Heinritz 2, Angelika Schall 1, Arndt-Peter Schulz*, 1
Article Information
Identifiers and Pagination:
Year: 2013Volume: 7
First Page: 78
Last Page: 85
Publisher ID: TOORTHJ-7-78
DOI: 10.2174/1874325001307010078
Article History:
Received Date: 11/1/2013Revision Received Date: 12/2/2013
Acceptance Date: 13/2/2013
Electronic publication date: 5 /4/2013
Collection year: 2013

open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.5/) which permits unrestrictive use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Background:
The aim of our study was to develop a test setup combining realistic force transmission with physiological movement patterns at a frequency that mimicked daily use of the elbow, to assess implants in orthopedic joint reconstruction and trauma surgery.
Methods:
In a multidisciplinary approach, an in vitro biomechanical testing machine was developed and manufactured that could simulate the repetitive forceful movement of the human elbow joint. The construction involved pneumatic actuators. An aluminum forearm module enabled movements in 3 degrees of freedom, while motions and forces were replicated via force and angular sensors that were similar to in vivo measurements.
Results:
In the initial testing, 16 human elbow joint specimens were tested at 35 Nm in up to 5000 cycles at a range of 10° extension to 110° flexion. The transmitted forces led to failure in 9 out of the 16 tested specimens, significantly more often in females and small specimens.
Conclusions:
It is possible to construct a testing machine to simulate nearly physiological repetitive elbow motions. The prototype has a number of technical deficiencies that could be modified. When testing implants for the human elbow with cadaver specimens, the specimen has to be chosen according to the intended use of the implant under investigation.
BACKGROUND
For many newly developed orthopedic implants, homologation or certification guidelines exist for preclinical testing. However, no such certification guidelines exist for endoprostheses or anatomically pre-contoured implants around the elbow joint that researchers or manufacturers could follow to ensure safe and reliable design of their inventions. Commonly, different material testing procedures are performed using the supposed main allocation levels of forces; thus, corresponding partners of artificial joints have to be tested individually.
In a review of the literature, a complication rate of elbow arthroplasty, amounting to 43% in long-term follow–up, has been described [1]. In that study, a high revision rate (18% on average) and a considerable rate (15%) of permanent complications were found. In very recent publications, overall failure rates, e.g., after elbow arthroplasty, have been described as 8% and 15% after 5 and 10 years, respectively [2]. A singular elbow implant has even been found to have a 70% failure rate in a retrospective study [3]. With these figures at hand, it becomes clear that devices for elbow surgery, unlike those for hips or knees, are still often used in humans without proper pre-market in vitro evaluation. This is most likely due to the fact that biomechanical testing devices, probably due to the complex elbow kinematics, are not readily available.
In the past, there have been attempts to create a physiological elbow testing apparatus [4-10]. These published test assemblies all focus on regeneration of the physiological movement and the force distribution of the corresponding joint partners. The applied forces are often weak and do not appear to mirror realistic force transmission. Also, the frequencies in the testing process are often not sufficient for the certification process of orthopaedic implants.
There are reported constructions describing promising results that can only apply up to 40 N in flexion and extension [6, 8, 9]. Others can test up to 95 N in flexion and about 70 N in extension, but restrict the test cycle to 5 sequences [4, 5] or test only isolated anatomical joint parts [7]. Another proposition was to apply realistic forces, but abandon physiological motion patterns [10]. All these approaches have their own merits, but are not useful tools in the development and testing of implants, as it cannot be assured that the newly designed devices have the right dimensions for the anatomical region they are destined for.
The aim of our study was to develop a testing machine combining realistic force transmission with physiological movement patterns at a frequency that mimicked daily elbow use in a postoperative clinical setting.
The underlying idea was that by this combination, important information could be gained about the failure mechanism and loosening tendencies of novel implants before human clinical trials are conducted. This study was conducted in cooperation with a manufacturer of osteosynthesis implants. This research-project was undertaken by a multidisciplinary team of medical device engineers, electronic engineers and physicians.
METHODS
Technical Development
The CAD-Program Solidworks 2009 (Dassault Systems, Stuttgart, Germany) was used for construction. The welded steel frame (Stainless steel A2 DIN 17440 and DIN EN ISO 3506) consisted of a central pillar of 3 welded 100-mm square bars (4 mm wall thickness), a frame of 40-mm square bars (3 mm wall thickness) and a base plate of a 5–mm thick steel (Fig. 1). The pneumatic actuators (MAS 40, Festo, Esslingen, Germany; for a detailed technical description see [11]) were mounted at the rear of the apparatus connected to a force sensor (1710DLL-2.5kN, Interface Inc., Scottsdale, Arizona, USA). Using Bowden cables (4 mm diameter, 9 x 17 –stranded wire, breaking limits 8300 N), the actuators were connected to the flexible test mount via deflection pulleys. These pulleys (MBGS60-2, Misumi Europa, Schwalbach, Germany), with pressed bearings, moved freely on axles (6 mm in diameter).
The forearm module was specifically constructed in a weight range of the human forearm of ca. 1.83 kg [12]. To achieve this, it had to be produced in Aluminum 7075 (Fig. 2). Employing four different types of springs (SWY24.5-45; SWU26-45; SWR26-45 and SWS26-45) of 45 mm length in a double spring module, forearm-flexor forces could be simulated in a range of 50 to 1264 N in a span of only 20 mm. The stranded wire was connected to the forearm module via lever arms of specific length directly connected to the specimen pot (Fig. 3). The connection to the spring module was achieved via a PEEK (Polyether ether ketone ) ball joint (internal diameter 12 mm, KGLM-12, Igus, Köln, Germany) to assure adjustment of rotational movements.
 |
Fig. (2). Forearm holding device. Completed forearm holding device with connected cables and angle sensor in front of the central pillar. |
 |
Fig. (3). Steel pot for fixing forearm with two lever arms for connecting cables. |
The upper arm of the specimen was also embedded in a steel pot with PMMA (Polymethylmethacrylat) resin (Technovit 4006 „HIGH CLEAR“, Heraeus Kulzer GmbH, Hanau, Germany) and adjusted according to the physiological anatomical axes. To avoid varus and valgus stress that is created by the natural flexion movement of the elbow joint [13, 14], the complete forearm module was fixed on a sliding plate at the central pillar, to ensure that lateral movements during flexion/extension were not counter-forced. Therefore, a physiological three-dimensional movement of the elbow joint was obtained.
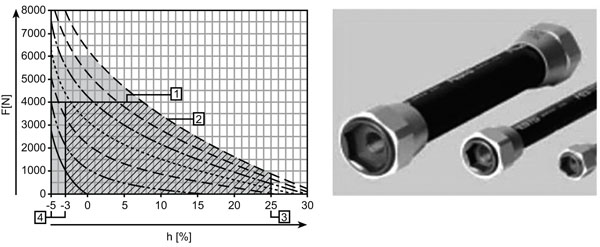
The pneumatic actuators, mimicking muscle function, had an operating pressure of 200 to 600 kPa and a force-elongation curve similar to human muscles [15] (Fig. 4).
A proportional–integral–derivative (PID)-control unit (PneusysII, Sincotec, Clausthal-Zellerfeld, Germany) with 3 monitoring and 3 control channels was used to control and monitor the movement and to monitor the forces. To ensure reliable monitoring of the movements, a no-contact angular sensor was implemented at the axis of the forearm module (POSIROT-Sensor, Version PRAS5, ASM, Moosinning, Germany). The maximal force was set to 1422 N. Using the software MuscleSim (Version 2.0.15, Festo, Esslingen, Germany), the appropriate actuator/muscle was determined to be the model MAS-40. This can be used over long periods at 250 kPa pressure. The actuators were alternatingly activated according to the signal of the angular sensor.
The adjustment of the control-parameter was determined in a test operating state. First static then dynamic optimization was performed using a sinusoidal signal. The outcome was a P-Factor of 3.18, an I-Factor of 3.0 and a D-Factor of 1.
Functional testing with specimens was conducted with 5000 cycles and a frequency of 0.6 Hz in a range of 0° to 110°. We chose this frequency according to Schuster [10], who showed that an active patient in a postoperative period of 5 weeks used the elbow every 5 minutes on average per 12 hours (5040 cycles). Although these movements are unlikely to cover the whole range of motion (ROM), this frequency simulates the “worst case scenario”. After 1000 cycles, the spring force was increased from 0 to 50 N, and after 2000 cycles, to 100 N. The specimens were visually inspected for failure after every 200 cycles. After 5000 cycles, the test was finished, the joints were harvested, opened and the joint surfaces were inspected.
Test Specimens
Sixteen human cadaver specimens (6 females, 10 males; age 63 to 90 years with a mean of 73 and an SD of 7.7) were used for testing and were ensured not to contain any pathological alterations (Tab.1). Joint capsule and ligaments were left intact, while the remaining soft tissue and skin were resected. The Bone Mineral Density (BMD) was measured with quantitative computer tomography (CT) (Siemens SOMATOM® DefinitionTM AS+, Erlangen, Germany). As the reference, the Mindways phantom was used (Mindways, Austin, TX, USA). The BMD was determined to have a mean of 158.7 mg/cm³ (SD 26.8). The sex specific difference (mean female specimen 143 mg/cm³, male 168 mg/cm³) was significant (p=0.032, Welch t-test). The bone size was measured in a calibrated CT image as the largest width over the epicondyles of the humeri. The mean value was 63.4 mm (56 to 73 mm). Female specimens had a mean of 56.7 mm, and the male ones 67.4 mm (significant different, p = 0.003, Mann-Whitney-U-test) (Table 1).
Characteristics of Cadaver Specimen and their Test Results
| Nr. | Sex | BMD mg/cm3 | Side | Age Years | Width in mm | Fracture |
|---|---|---|---|---|---|---|
| 1 | male | 198 | left | 71 | 69 | no |
| 2 | male | 128 | left | 67 | 70 | no |
| 3 | male | 155 | right | 72 | 73 | no |
| 4 | male | 174 | right | 74 | 68 | no |
| 5 | male | 145 | left | 72 | 73 | no |
| 6 | male | 149 | left | 74 | 68 | no |
| 7 | male | 222 | right | 67 | 70 | no |
| 8 | male | 193 | right | 71 | 69 | no |
| 9 | male | 173 | left | 90 | 57 | yes |
| 10 | male | 144 | right | 90 | 57 | yes |
| 11 | female | 126 | right | 76 | 57 | no |
| 12 | female | 134 | left | 76 | 57 | yes |
| 13 | female | 140 | right | 63 | 56 | yes |
| 14 | female | 150 | right | 71 | 57 | yes |
| 15 | female | 154 | left | 71 | 57 | yes |
| 16 | female | 154 | left | 63 | 56 | yes |
Before testing, the specimens were slowly warmed to 20° C and were constantly kept moist. The joint axis for flexion and extension of the elbow joint was marked with a K-wire. The embedding of the forearm shaft could therefore be adjusted with a laser cross. The forearm was embedded in a neutral position of pro-/supination.
Statistical Analysis
Statistical analyses were performed with the software SPSS-Statistics (Version 19, IBM-SPSS, Chicago, USA). The correlation of the width of the bone, sex, age and BMD to frequency of bone fracture was tested by Kendall because of the small sample size.
RESULTS
Facilitating indirect force transmission via cables and pulleys, it was possible to transmit up to 450 N in flexion and 640 N in extension (Fig. 5). The direction of the cables, thus, represented the force vector (Fig. 2) of the acting forces, while the distance to the rotational center of the elbow joint represented the lever arm length per flexion movement (Figs. 3, 6 and 8), which varied between 3.5 and 8.2 cm for flexors and 3.0 and 4.8 cm for extensors. With these figures (Fig. 7), the torque was calculated. Maximum torque in flexion was 35.3 Nm, and 30.7 Nm in extension. The resulting torque combining flexor and extensor moments was 11.2 Nm.
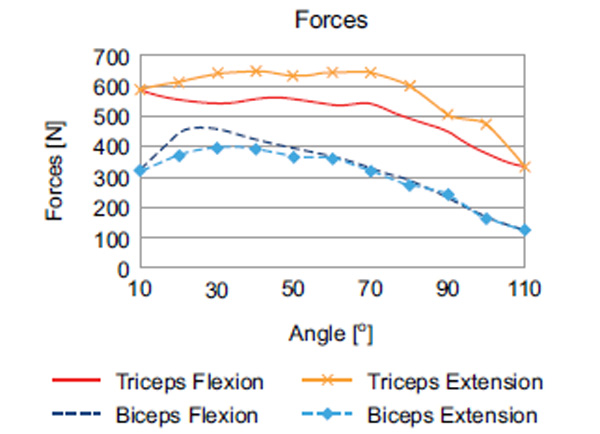 |
Fig. (5). Experimental forces of extensors and flexors (MAS 40) in flexion and extension. |
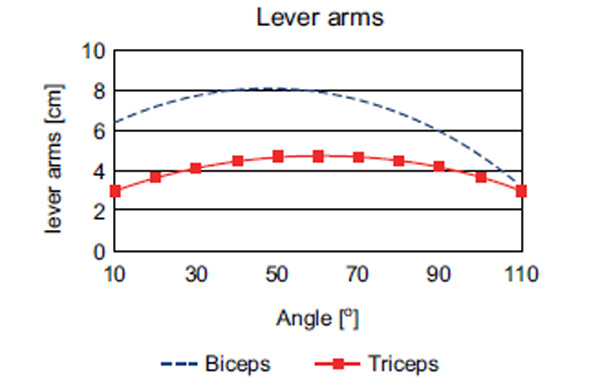 |
Fig. (6). Changing of lever lengths of specimen flexors and extensors from 10° to 110° (without an algebraic sign change). |
 |
Fig. (7). Absolute and resulting torques (Nm) of moving specimens from 10° to 110° of flexion. |
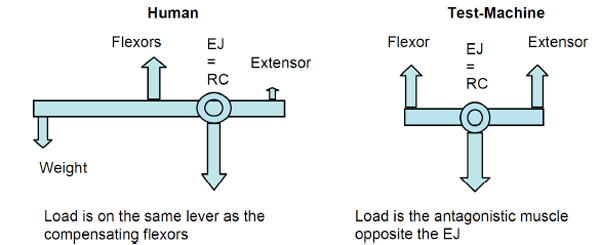 |
Fig. (8). Relation of power vectors in situ and in the test machine (EJ = Elbow Joint, RC = Rotational Centre). |
Curve line in flexion (Fig. 7):
Arm moving is a forced swaying. On starting flexion at 10°, the speed was 0 and acceleration maximal. The system had to overcome inertia and gravity to achieve maximum speed. Acceleration was an application of a torque. When maximum speed was reached, the speedup ended and no torque was effective. The system was in a dynamic balance after flexion from 10° to 70°. To avoid swaying beyond the endpoint, the arm motion had to be slowed. Slowing is a negative speedup and thus, a negative torque. Maximum torques (on flexion from 12.8 Nm to - 6.02 Nm) were expected to be uniform, but due to gravity, they were not. Gravity dulled the system and supported retardation of flexion, resulting in a lesser demand of power. At the endpoint, the speed again was 0 and acceleration minimum (negative maximum).
Curve line in extension.
The conditions were similar to flexion. However, with reverse action, rotation was inverted. Thus, negative moments increased and positive moments decreased speed. The starting point was 110°. Due to gravity, less power had to be put into the system to overcome inertia.
The maximum speed was present after 60° extension (i.e., at 50° flexion). From there, a positive moment acted as a slowing moment and the arm stopped after extending 100° (i.e., in 10° flexion).
At the center of the motion cycle, i.e., at 50° flexion, the load on the elbow joint could be calculated, assuming a quasi-static equilibrium as the lower arm moves in the machine with constant speed. The flexor (396 N) and extensor (557 N) forces in the testing machine were measured at 50° while performing the motion cycle between 10° and 110° of flexion.
Although it was initially planned to design a testing device with a ROM of 0° to 110°, we had to reduce the range because of the mostly geriatric specimens. The planned motion speed of 1.5 sec for a complete cycle was achieved with a frequency of 0.67 Hz.
After 5000 cycles, only 9 of the 16 specimens remained fully intact. Most alterations were found at the coronoid process (for details, see Table 1). Eight of the ten male but only one of the six female specimens were left intact after the test cycle.
Statistical Analysis
Kendall correlation analysis did not find a connection between failure of the specimen and age or BMD. Specimen size and sex on the other hand correlated significantly with a fracture during the testing process.
We found that female specimens fractured significantly more often than male ones (p = 0.049, Fisher’s exactly test, Bonferroni-corrected). Fractures around the elbow correlated inversely with the width of the humerus over the epicondyles in cadaver measurement (τb = 0.73, p = 0.001) (Table 2).
Correlation According to Kendall from Age, BMD, Sex and Width of Bone to Frequency of Fracture and Level of Significance
| Correlation Coefficient τb | p-Value (2-Sided) | |
|---|---|---|
| Age | -0,0242 | 0,9147 |
| BMD | 0,1963 | 0,3679 |
| Sex | 0,6181 | 0,0167 |
| Width | 0,7307 | 0,0015 |
DISCUSSION
The presented elbow simulation test stand is so far the only published construction that allows the testing of human elbow specimens with forces that realistically mimics movements in a realistic range of motion.
Function was tested in 16 human cadaver specimens. As a result, we found that the construction of the device was possible, but there were deficiencies that restricted the application. The operation of the actuators with only one channel and with only one force sensor was not sufficient to down-regulate forces for applications that require testing of geriatric specimens or simulate less forceful movements. The currently applied forces of up to 35.3 Nm are in the upper range of the naturally occurring forces in men [16], this became especially clear when testing the significantly smaller female specimens.
Considering an equilibrium of the flexor and extensor moments and the moment of the lower arm partial weight of the test machine (approx. 5 kg, with a lever arm of approx. 10 cm in 50° flexion), the force on the elbow joint was 895 N.
Calculation of an equivalent additional weight:
Due to the changed lever arms in the testing machine, equivalent additional weight acting on the hand in the physiological elbow could be calculated to estimate the load simulated by the testing machine (Fig. 8). Considering an anatomical lever arm of the flexors (lflex) of 3.2 cm [12], a lever arm of the M. triceps (ltri) of 2.3 cm [17], a typical weight of the lower arm of 1.83 kg with a lever arm (lla) of 15.6 cm [12] and a lever arm of 30 cm from the elbow joint to the hand (23 cm in 50° of flexion laew), the static load acting on the elbow joint could be calculated. Assuming an antagonistic force of the M. triceps to be 40% of that of the M. biceps [18] and a contribution of the M. biceps to be 25% of that of the flexor force [17], the antagonistic force of the M. triceps was 10% of the overall flexor force.
In a static condition, the flexor (Fflex*lflex) and extensor (Ftri*ltri) as well as the moment of the lower arm (Fla*lla) and of the additional weight (Faew*laew) are in equilibrium. Moreover, the sum of the physiological flexor and extensor forces, the weight of the lower arm and the additional equivalent weight (Faew) have to be equal to the joint load (Fej) in the testing machine. Therefore:
The applied torque was equal to a simulated lift of 11 kg held in the hand in 50° flexion, taking the antagonising muscle into account.
It was our aim with this first version of the testing machine to simulate a period of bone healing, such as fracture consolidation. We used the rationale that was described by Schuster [10]. When it comes to testing artificial joint components in the future, the frequency of testing will have to be increased.
The duration of 1.5 sec for a complete motion cycle achieved a speed equal to that described for humans [19]. The main functional ROM of the human elbow has been described in vivo to be 30° to 130° [20], a range that is nearly reflected by our device.
Correct alignment of the humero-ulnar joint axis is crucial for undisturbed testing. The used method of first marking with K-wires and then alignment with Laser-cross marking during fixation is somewhat time consuming; an automatic or semi-automatic alignment of the test stand should be implemented instead.
Force transmission of the hand via the forearm onto the elbow joint are distributed unequally [21, 22] and require realistic simulation of both the ulna and radius [23]. The drawback of this test setup was that we had to omit forearm rotation movements; it is possible though to define which position the forearm is tested in.
By implementation of pneumatic actuators, we could mimic force patterns that were comparable to human movements, which has been evaluated in the past [11]. The force-elongation curve of biological and pneumatic muscles are comparable [24], although the individual pattern of singular muscles cannot be reproduced in detail and pneumatic muscle has a pattern that is more comparable to the biceps than the triceps in vivo [15].
The mean BMD in our test specimens was low at 159 mg/cm3 when compared to a study with a comparable mean age (276 mg/cm3) [10].
The use of human specimens instead of artificial components means that a certain variance has to be taken into calculation. Yet, this test method directly used the physiological region of interest, thus not requiring elaborate methods of verification and validation. It is important to use cadaver specimens that reflect the intended patient population of the implant under investigation. The current setup of the test device can test implants and devices for a younger and more active population. It is unrealistic to test the force of a shopping bag of 11 kg held by the hand with a medical device that is intended for elderly people, e.g., for the treatment of osteoporotic fractures. The forces that were applied in this study were equal to what can be expected with double or single-handed push-ups [25]. Torques of up to 61 Nm have been observed in professional baseball players [26].
One of the results was that fracture incidence around the elbow correlated to the width of the humerus over the epicondyles. This has not been described before and warrants further studies. Furthermore, we found that female specimens fractured significantly more often than male ones. This reflects the higher forces transmitted in male elbows in vivo and has been investigated before [16, 27, 28]. Systematic studies of fracture resistance of bone has not often been investigated, but results have shown that female bone is less fracture resistant than male bone [29]. Although it has been described that BMD has an impact on bone fracture resistance [30] in some body regions, we did not find a correlation in our study (Table 2).
The following modifications of the described apparatus are necessary to facilitate testing of a wide range of devices in different patient populations:
- The range of possible motion is sufficient for extension; the flexion can be increased by modification of the embedding pots, which would need an elliptic shape.
- A dual control system is required for the muscle actuators including two valves.
- A self-adjusting mechanism for the alignment of the specimen would be desirable as the currently used technique is time consuming and involves radiation.
The first two modifications are technically not demanding and are already developed. The third modification is, at the moment, not possible without large technical modifications, which would make the device technically very demanding and increase costs.
Comparing our results to the literature, we found several devices that attempted physiological testing of the elbow joint. Sjöbjerg described in 1987 [31] the testing of joint instabilities of the elbow using 1.5 Nm stress and a specimen fixed in steel containers. Morrey in 1991 [32] was the first to use a test apparatus that mimicked m. biceps, m. trizeps and m. brachialis forces using nylon ropes. By applying a force of approximately 20 N each, forces were created that occurred in vivo in active elbow motion without further loads. Inagaki [33] increased loads in an advancement of the apparatus to 60 N in extension and flexion, enabling 3 cycles per test series.
Bottlang [34] developed a device to determine the rotational axis of the elbow joint. A force transmission of 2 N via flexors and 20 N via extensors, or vice versa, was possible. A single cycle lasted approximately 4 seconds (32°/sec).
Johnson [5] constructed a device that implemented pneumatic actuators via cables attached to ligaments (Mm.Biceps, Brachialis, Brachioradialis, Pronator teres and Triceps) using forces of 15 to 58 N per ligament. A further test device was developed by Safran [35], which fixed the joint in a specific angle and then tested valgus or varus stress at the elbow joint.
None of these described devices are capable of repetitive testing of orthopedic devices at the elbow joint, since the applied loads seldom reach physiological ranges. The number of test cycles of these devices was incapable of mimicking a long-term load situation.
CONCLUSIONS
We achieved our aim of developing a test stand combining realistic force transmission with physiological movement patterns at a frequency that mimics daily elbow use. The device needs further modification to gain its full potential in biomechanical studies.
AUTHORS` CONTRIBUTIONS
All authors were fully involved in the study and preparation of the manuscript. JK designed the test device, wrote parts of the article and lead the cadaveric experiments. RW performed the technical parts of the device and statistical calculations. MH build the devise and performed initial testing. AS prepared cadaver specimen and tested these. APS was involved in the initial idea, the test design and preparation of the manuscript. All authors read and approved the final manuscript and concurs with the content in the manuscript.
AUTHORS` INFORMATION
JK and APS are employed as consultants in the trauma center of a university hospital. RW is working as an engineer and leads the biomechanical laboratory of the department of trauma and orthopedic surgery in Lübeck. MH is working as a medical engineer at the same institution. AS is working as a physician at the university medical center.
CONFLICT OF INTEREST
This work was financially supported in part by Litos GmbH (Ahrensburg, Germany). The Litos GmbH had no involvement in the analysis and interpretation of data, writing of the manuscript or in the decision to submit the manuscript for publication.
The authors disclose any financial and personal relationships with other people or organizations as named that could inappropriately influence our work.
ACKNOWLEDGEMENTS
The authors thank Dr. Roman Nassutt (CEO Litos GmbH) for his support in developing the testing machine and Dr. Friedrich Pahlke for his help in statistical analysis and Prof. Rüdiger Döhler for proof reading. We acknowledge the Anatomical Institute of University in Lübeck (Prof. L.C. Busch) for allocation of the human cadaveric elbow joints.