All published articles of this journal are available on ScienceDirect.
Variation of Anatomical and Physiological Parameters that Affect Estimates of ACL Loading During Drop Landing
Abstract
Background:
Anterior cruciate ligament (ACL) loading during drop landing has been recently studied with a sagittal plane knee model developed by Kernozek and Ragan using mean anatomical and physiological parameters obtained from cadaveric and clinical data. It is unknown how estimates in ACL load may be altered due to variations in anatomical and physiological parameters used from other research.
Methods:
Using the same model, these parameters were systematically varied, including: tibial slope, moment arms of the patellar tendon, hamstring, and gastrocnemius at the knee and ankle, patellar tendon and hamstring line of force, ACL stiffness, and nonlinear muscle activation parameters. To determine the sensitivity of the model to changes in these parameters, each was varied independently by ±5% and by ranges reported in the literature. Changes in maximum ACL load and shear force components of the patellar tendon, hamstring, and tibio-femoral contact force were calculated from drop landing data of 21 subjects.
Results:
The variation in ACL load during drop landing from its nominal value was largest (-100% to 176%) when extremes in reported tibial slope values were utilized. Variation in the next most important parameter, patellar tendon line of force, affected ACL load by -72% to 88%.
Conclusion:
Variations in tibial slope and patellar tendon line of force had the greatest influence on estimated ACL loading during drop landing. Differences in these parameters between subjects may be just as important to ACL loading as the kinematic and kinetic performance differences observed in landing.
INTRODUCTION
Anterior cruciate ligament rupture is one of the most debilitating and prevalent injuries among athletes. The mechanisms and risk factors of non contact ACL injury have been investigated to develop injury reduction and prevention strategies [1, 2]. Several anatomical, biomechanical, hormonal, and environmental risk factors have been shown to be important in the etiology of ACL injury [1, 3]. Loading of the ACL is complex during high risk movements and injuries are thought to occur due to aberrant loading in the sagittal, frontal, transverse or in combination [4].
Computer models allow the researcher to estimate loads in muscles and on specific tissues and intra-articular structures during dynamic tasks that are very difficult to measure via cadaveric testing or in vivo with surgically implanted transducers. The investigator can manipulate various parameters and then directly determine their influence on estimations of ACL loading. Many current biomechanical investigations largely use discrete kinematic (ie. Knee flexion at initial contact, peak knee abduction angle) or kinetic (i.e. Peak knee abduction moment) parameters to speculate on how the ACL may be loaded during landing or cutting tasks. The inverse dynamics approach yields only net moments and reaction forces and not tissue specific loads. Pflum et al. [5], using a much more sophisticated three dimensional model of the knee to study drop landing, reported that the main factors influencing ACL force were patellar tendon and compressive loading at the tibiofemoral joint. Their findings implicate the potential use of a more simple two dimensional model. Torry et al. [6] reported that the knee shear joint reaction force and extensor moments were not related to peak anterior or lateral translation between the tibia and femur obtained with biplane fluoroscopy during drop landing. Taking the findings of Pflum et al. [5] and Torry et al. [6] together, it may be possible that simple two dimensional models can provide insight to the rather complex interaction of forces applied during human performance studies that describe ACL loading during landing. Kernozek and Ragan [7] developed a sagittal plane model of the knee to estimate ACL loading during drop landing from kinematic, kinetic, and electromyography (EMG) measurements. This model uses equations based on anatomical and physiological input parameters in addition to laboratory drop landing measurements to estimate ligament, muscle, tendon, and bony forces in the knee. These parameters are taken from existing literature sources and incorporated into knee models to provide dynamic estimates of these loads. The extent to how these anatomical and/or physiological parameters may affect sagittal knee loading estimates during drop landing has not been explored. Imaging studies have reported the relative importance of tibial slope in describing individuals that sustained an ACL tear [8-11]. Patellar tendon angle relative to the tibial shaft has been reported to increase anterior tibial femoral shear forces during quadriceps activation while hamstring forces through their tibial attachment are thought to provide reductions in anterior tibiofemoral shear [5, 12, 13]. It is unknown how the systematic variation in these parameters may influence ACL loading estimates in drop landing. Therefore, the purpose of this investigation is to examine the variability in model predictions of ACL loading and anterior-posterior (AP) knee forces during drop landing performance due to variability in reported anatomical and physiological parameters. The parameters that had the most potential to influence the two dimensional nature of the model were evaluated.
MATERIALS AND METHODS
Subjects and Testing Protocol
Motion analysis (Eight Eagle Digital Cameras with Cortex Software, Motion Analysis Corporation, Santa Rosa, CA, USA), force platform (Model 4060, Bertec Corporation, Columbus, OH), and EMG (Bagnoli 8, Delsys, Inc., Boston, MA, USA) data of the hamstrings from 21 healthy female students with no history of knee injury or chronic knee pain (age range = 18-24, mean height = 169.46 (SD 6.12) cm, mean weight = 63.83 (SD 8.30) kg) were normalized and averaged. These kinematic, kinetic data from inverse dynamics analysis and hamstring EMG data were processed in the same manner as previously described and used as input to the Kernozek & Ragan model [7]. This Each participant dropped from a hang bar at a height of 40 cm, measured from the force platform to the bottom of the subject’s shoe while parallel to the ground. Subjects landed using both legs in a toe heel pattern for five consecutive trials after performing three practice trials. Each participant performed three isometric strength tests for the hamstrings at two body positions as previously described on a HUMAC Cybex Norm Isokinetic dynamometer [7]. Based on the averaged processed hamstring muscle activation data these data were used to calculate the relative amount of hamstring tension based on hamstring EMG data in drop landing. Informed consent was provided by each subject per university guidelines prior to participation.
Anatomical and Physiological Parameters
The anatomical and physiological parameters chosen for analysis were those that had the greatest potential to influence model predictions (i.e. those that appeared in the AP force and moment equations). These parameters were tibial slope; hamstring and patellar lines of force at full knee extension along with the rate of change in these lines of force with respect to knee flexion (Fig. 1); the moment arm of the patellar tendon, the moment arms of the gastrocnemius at the knee and ankle, initial moment arm of the hamstring as well as the rate of change in the hamstring moment arm with respect to knee flexion; ACL stiffness; and nonlinear muscle activation parameters [14].
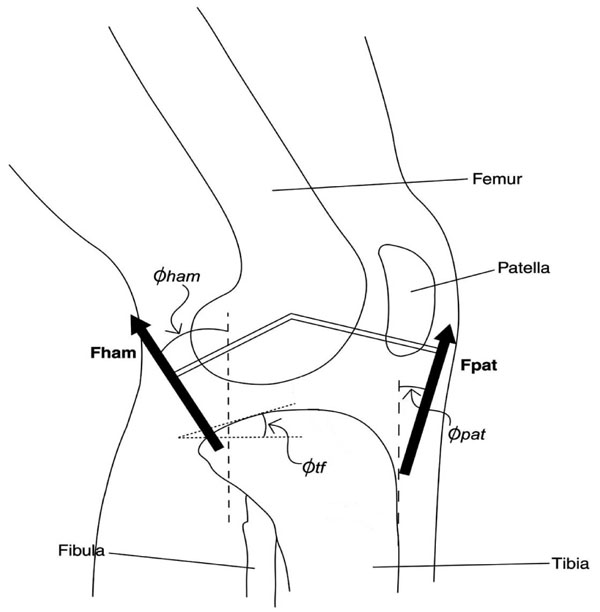
Selected anatomical parameters [hamstring line of force (Φham), patellar tendon line of force (Φpat), and tibial slope (Φtf)] examined in the model for drop landing are depicted.
The model outputs examined were maximum ACL tension (FaclMAX) and the maximums of the AP forces that contributed to ACL loading during drop landing (i.e. shear force components of the ankle reaction force, patellar tendon, hamstring, and tibio-femoral contact force).
Sensitivity Analysis
To assess model sensitivity, selected anatomical and physiological parameters were varied from the original data used in Kernozek and Ragan [7]. Each parameter was adjusted from the initial input value independently. Linear parameters (e.g. patellar tendon moment arm) were varied by ±5% and angular parameters (e.g. tibial slope) were varied by ±0.05 radians (2.9º) (Table 1). FaclMAX and AP force values were then calculated based on the variation in each parameter.
Anatomical and Physiological Parameters and the Amount that they were Varied (Control ± 5% or ± 2.9°) in the Knee Model for Drop Landing Trials
| Parameter | Control | +5% | -5% |
|---|---|---|---|
| Initial Moment Arm (cm) | |||
| Patellar tendon | 4.00 | 4.20 | 3.80 |
| Gastrocnemius (knee) | 2.50 | 2.63 | 2.38 |
| Gastrocnemius (ankle) | 5.30 | 5.57 | 5.04 |
| Hamstring | 3.00 | 3.15 | 2.85 |
| Change in Moment Arm (cm/Degrees Knee Flexion) | |||
| Hamstring | 1.50 | 1.58 | 1.43 |
| ACL stiffness (N/mm) | 216 | 226.8 | 205.2 |
| Nonlinear activation parameters | 1.70 | 1.785 | 1.651 |
| Parameter | Control | +2.9° | -2.9° |
| Tibial slope (degrees) | 8.5 | 11.4 | 5.6 |
| Initial Line of Force (Degrees) | |||
| Hamstring | 6.00 | 8.90 | 3.10 |
| Patellar tendon | 15.0 | 17.9 | 12.1 |
| Change in Line of Force (Degrees/Degrees Knee Flexion) | |||
| Hamstring | 1.00 | 1.05 | 0.95 |
| Patellar tendon | 0.192 | 0.215 | 0.170 |
Anatomical and Physiological Variation
Once the sensitivity of the model’s outputs to each anatomical and physiological parameter was evaluated, parameters that yielded the greatest percentage change in model outputs were further examined. Model calculations were also performed on the drop landing data using the maximum and minimum published anatomical values.
RESULTS
Participants landed with an average hip angle of 3.5 degrees of flexion ± 4.1 degrees, knee angle of 9.2 degrees of flexion ± 3.8 degrees and ankle plantar flexion angle of 18.5 degrees ± 10.2 degrees. The model was most sensitive to a change in tibial slope and patellar tendon line of force; particularly for FaclMAX (Fig. 2). The tibial slope, when varied by ±0.05 radians, yielded the greatest change in FaclMAX of ± 69%, while the ± 5% variation in patellar tendon line of force yielded a change in FaclMAX of -43 to 45%. The next most important parameters were patellar tendon line of force (ΔΦpat) with knee flexion angle and patellar tendon moment arm (ptma). The ΔΦpat resulted in a change in FaclMAX of 15% while ptma yielded a change in FaclMAX of 10%. All other anatomical and physiological parameters had an influence on ACL loading of less than 5%.
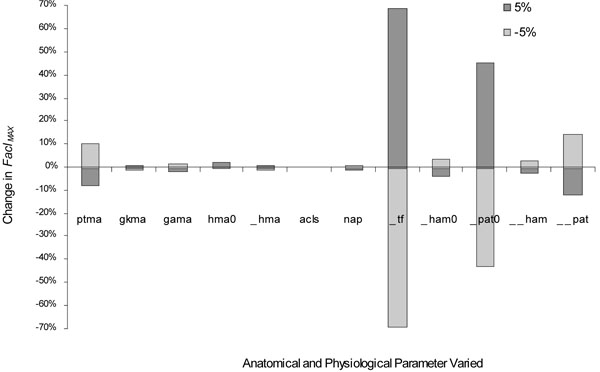
Percent change in FaclMAX due to changes in the following anatomical and physiological parameters: moment arms of the patellar tendon (ptma), gastrocnemius at the knee (gkma), and ankle (gama), initial hamstring (hmao) and change in hamstring angle (Δhma); ACL stiffness (acls); nonlinear activation parameters (nap); tibial slope (Φtf ); initial line of force of the hamstring (Φhamo) initial patellar tendon line of force (Φpat), rate of change in the hamstring angle (ΔΦham) with knee flexion, and rate of change in the patellar tendon line of force (ΔΦpat) with knee flexion. Distance measures were changed by ±5%. Angular measures were changed by 0.05 radians (±2.9°). Δhma, ΔΦham, and ΔΦpat are with respect to change in knee flexion, initial values at those at full knee extension.
Model output for anterior shear force components that resulted in ACL tension were examined. The model output of maximum patellar tendon and tibio-femoral shear force showed the greatest sensitivity to the tibial slope, varying by -58 to 54% and -34 to 38% respectively. Variation in the patellar tendon line of force did not affect the tibiofemoral shear force but yielded a change in patellar tendon maximum shear force of -69 to 34%.
Since the estimated ACL load appeared to be strongly influenced by variation in tibial slope and the patellar tendon line of force at full knee extension, model outputs were further examined using extremes from published data (Table 2). Using a range of published tibial slope values of 1º to 15º yielded a change of FaclMAX between -100% to 176%. For tibial slope of 1º the model predicted that the ACL was not loaded during drop landing. The published patellar tendon line of force values ranging from 10º to 20º resulted in a change in FaclMAX of -72% to 88%.
Minimum and Maximum Anatomical Data for the Tibial Slope (Φtf ) [15] and Patellar Tendon Line of Force (Φpat) [16] are Reported with the Corresponding Maximum ACL Tension (FaclMAX) in Body Weight, Maximum Patellar Tendon Shear Force (FptMAX) in Body Weight, Maximum Tibio-Femoral Shear Contact Force (FtfMAX) Body Weight, As Well As the Percent Changes in these Maximum Model Outputs from the Control Values. Control Anatomical and Activation Parameters Values were from Kernozek and Ragan [7]
| Control | Tibial Slope (Φtf) | Patellar Tendon Line of Force (Φpat) | |||
|---|---|---|---|---|---|
| Minimum | Maximum | Minimum | Maximum | ||
| Parameter input value | 1.0° | 15.8° | 10° | 20° | |
| FaclMAX | 0.2563 | 0 | 0.7066 | 0.07234 | 0.4823 |
| Percent change in FaclMAX | -100% | 176% | -72% | 88% | |
| Fpt | 0.3298 | 0.7509 | -0.24 | 0.122 | 0.5397 |
| Percent change in FptMAX | 128% | -173% | -63% | 64% | |
| Ftf | 1.056 | 0.1208 | 2.122 | 1.034 | 1.046 |
| Percent change in FtfMAX | -89% | 101% | -2% | -1% | |
DISCUSSION
Kernozek and Ragan [7] reported a 73% variation in ACL loading across subjects during landing. The majority of these differences were attributable to variation in kinematic and kinetic data between subjects. The current study indicates that variability in tibial slope and patellar line of force had an equally large role on ACL tension.
The finding that a larger tibial slope increases ACL loading is supported by several studies [8-12]. When the maximum tibial slope of 15.8° from de Boer et al. [15] was used, our model predicted that ACL loading would increase 176% during drop landing compared to the control data. Dejour and Bonnin [17] and Yeow et al. [18] concluded that greater tibial slope leads to a larger anterior tibiofemoral shear force increasing ACL tension during joint compressive loading. Our results suggest that increases in tibial slope result in greater ACL loading during drop landing where compressive loads are high. This finding is also supported also by Pflum et al.’s [5] study using a more sophisticated three dimensional knee model simulation of drop landing.
Our findings support previous studies that have related patellar insertion angle to ACL tension (e.g. Herzog and Read [16]; Pflum et al. [5], Shin et al. [19]; Shin et al. [20], Torzilli et al. [21]). The force of the quadriceps, applied through the insertion of the patellar tendon on the tibia, generates a shear force resulting in ACL tension [5, 18]. ACL ruptures have often been reported near or at full knee extension where greater patellar tendon line of force increases the anterior shear component associated with quadriceps shortening [2, 16]. When the maximum patellar tendon line of force of 20° from Herzog and Read [16] was used, our model predicted that ACL loading would increase 88% during drop landing compared to the control data. Nunley et al. [13] reported larger patellar tendon angles in females as compared to males. It appears that this angle increases the shear component of the quadriceps force applied to the tibia throughout the entire range of knee motion during landing.
The main limitations of this study were the use of a simple 2-D knee model and the manner in which the anatomical and physiological parameters were independently varied. The use of a more complex model that better incorporates the intricate medial and lateral surface geometry of the tibia [8, 11] and patellar tendon line of force may be warranted. Hashemi et al. [8] reported that females with increased lateral tibial slope combined with decreased medial tibial depth had a greater risk of suffering ACL injury. Also, further studies could use subject-specific measurements of parameters, in particular tibial slope and patellar tendon line of force, due to the complex relationship that may exist between these two parameters and ACL load during impact related activities.
CONCLUSION
This study evaluated the change in knee sagittal plane model estimations of ACL load during drop landings due to the variation of anatomical and physiological parameters. Although most of the parameters examined resulted in only small affects on model outputs, the tibial slope and patellar tendon line of force were shown to have greatest influence on ACL load. Estimations using the maximum and minimum tibial slope and patellar tendon line of force values reported in literature resulted in up to 2.8 and 1.9 fold increases in ACL loads respectively. Variability in tibial slope and patellar tendon angle appear to have as large an influence on ACL tension as the kinematic and kinetic variability observed in drop landing studies. Further development of modeling efforts appear warranted that incorporate more complex knee geometry and multi-planar loading scenarios.
ACKNOWLEDGEMENT
This study was partially funded by the Hi-Tech funding initiative from the State of Wisconsin.
CONFLICT OF INTEREST
There are no reported conflicts of interest for this investigation.


