All published articles of this journal are available on ScienceDirect.
Ninety-Degree Chevron Osteotomy for Correction of Hallux Valgus Deformity: Clinical Data and Finite Element Analysis
Abstract
Hallux valgus is a very common foot disorder, with its prevalence estimated at 33% in adult shoe-wearing populations. Conservative management is the initial treatment of choice for this condition, but surgery is sometimes needed. The 600 angle Chevron osteotomy is an accepted method for correction of mild to moderate hallux valgus in adults less than 60 years old. A modified 900 angle Chevron osteotomy has also been described; this modified technique can confer some advantages compared to the 600 angle method, and reported results are good. In the current work we present clinical data from a cohort of fifty-one female patients who had surgery for sixty-two hallux valgus deformities. In addition, in order to get a better physical insight and study the mechanical stresses along the two osteotomies, Finite Element Analysis (FEA) was also conducted. FEA indicated enhanced mechanical bonding with the modified 900 Chevron osteotomy, because the compressive stresses that keep the two bone parts together are stronger, and the shearing stresses that tend to slide the two bone parts apart are weaker, compared to the typical 600 technique. Follow-up data on our patient cohort show good or excellent long-term clinical results with the modified 900 angle technique. These results are consistent with the FEA-based hypothesis that a 900 Chevron osteotomy confers certain mechanical advantages compared to the typical 600 procedure.
INTRODUCTION
Hallux valgus is one of the most common foot disorders in civilized populations [1], with an estimated 33% of adults in shoe-wearing populations having some degree of this condition [2]. Hallux valgus can be treated conservatively or operatively, but the non-operative approach is considered as the first-line option [3].
More than 150 surgical procedures have been described for hallux valgus treatment [2]. Distal metatarsal Chevron osteotomy is indicated for correction of mild to moderate hallux valgus (if the hallux valgus angle is less than 300 and the intermetatarsal angle is less than 150 with a congruent metatarsophalangeal joint). The typical Chevron osteotomy (depicted as BCB’ in Fig. 1) has a simple 600 angle and is very popular, because it provides stability, rapid healing and minimal shortening with a low complication rate [4-10]. Even though this is a successful technique for hallux valgus, more than a hundred versions of distal osteotomy have been described [1]; the large number of proposed techniques indicates that none of these techniques is entirely satisfactory, and there is certainly room for improvement.
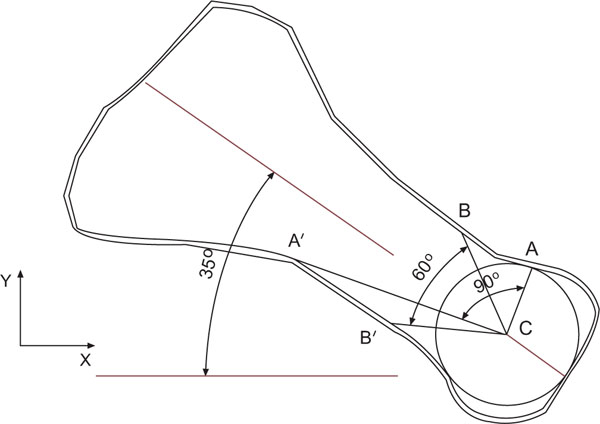
Two dimensional side views of two Chevron osteotomies applied at the metatarsal bone of the first ray in the human foot: Points BCB’ depict the classic 600 osteotomy, whereas points ACA’ depict the proposed 900 osteotomy. Point C indicates the center of the circle circumscribed to the bone head.
Finite element analysis (FEA) is a computational tool that is often used for structural analysis of mechanical systems [11]. In recent years, FEA is increasingly used in the biomedical sciences, with several applications of this methodology recently published, especially in dentistry [12] and in orthopaedic surgery [13, 14]. In the current work we present clinical data and FEA results for a 900 Chevron osteotomy (depicted as ACA’ in Fig. 1). FEA results predict strong mechanical bonding for the 90o osteotomy, with enhanced compressive stresses that keep the two bones together, and reduced shearing stresses that tend to slide the two bones apart, compared to the 60o method. As our clinical data are very encouraging, and consistent with FEA results, we hope this new technique will contribute to improved patient comfort and quality of life.
MATERIALS AND METHODOLOGY
Patient Population and Procedure
This was a prospective observational cohort study on fifty-one female patients with sixty-two hallux valgus deformities, who had the modified 900 chevron osteotomy in our institution between 1997 and 2003. As this is an observational cohort study, there was no control group and no blinding. The research protocol was approved by the University of Patras Ethics Committee, and all patients gave written informed consent before enrolling in the study. All procedures were carried out by the same two orthopaedic surgeons under general endotracheal anesthesia, and a tourniquet was used in all cases. The procedure started with a medial slightly curved longitudinal incision, followed by a Y-shaped capsulotomy, and exposure of the medial prominence. The exostosis was then removed, and all patients had a modified 900 Chevron osteotomy (Fig. 2) fixed with a Hebert screw. The capsule was closed and placation of the medial capsule was performed. Any lesser toe abnormalities were also corrected during the operation.
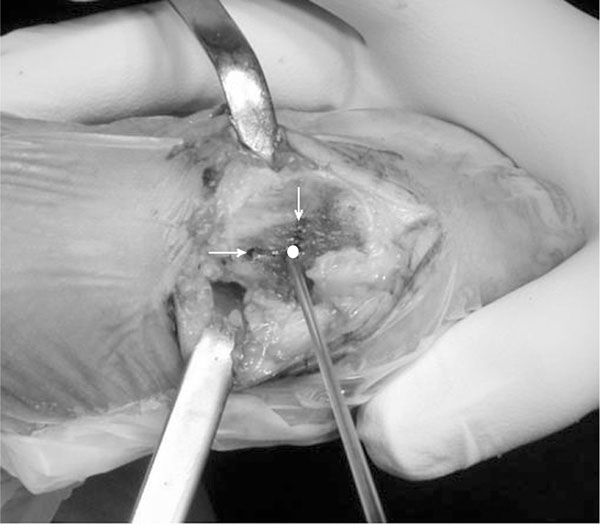
Photograph taken during a 90o distal metatarsal osteotomy. The actual 90o osteotomy looks like an “L” shape, as marked by the arrows and circle.
Mean patient age was 54.9 years (range 17-70 years) and mean length of follow-up was 32.7 months (range 24-54 months). On their last follow-up visit, patients were interviewed and had clinical and radiologic evaluation, including weight-bearing antero-posterior and lateral radiographs, intermetatarsal angle (IMA) and hallux valgus angle (HVA) measurement, and comparison with preoperative films. All patients were examined according to the AOFAS Hallux Metatarsophalangeal-Interphalangeal Scale [15]. They were questioned about pain, function, activity limitations, and footwear requirements and examined to assess alignment, metatarsophalangeal joint motion, interphalangeal joint motion and callus formation. According to this scale, scores between 93 and 100 points indicate an excellent result, 83 to 92 points indicate a good result, 66 to 82 points indicate a fair result and scores less than 65 points are evidence of a poor result.
Finite Element Analysis
In an attempt to better understand the physical consequences of the modified procedure and, hopefully, predict clinical results, Finite Element Analysis (FEA) was used to calculate the distribution of stresses on the first ray of a human foot bone model. According to FEA a mechanical model of a body is divided into numerous finite geometrical elements; then the equations of the theory of elasticity are applied to these elements. Due to the finite size of these elements, the differential equations can be approximated by equations of difference which can be solved algebraically by numerical methods. In order to improve consistency, we used two different standard FEA software packages: ANSYS WorkbenchTM 10.0 (ANSYS, Inc. Southpointe, 275 Technology Drive, Canonsburg, PA 15317, USA), which is a commercial software package, and OOF2, which is an open-code freeware from the National Institute of Standards and Technology (http://www.nist.gov/index.html). The acronyms “ANSYS” and “OOF” are used in this work when referring to these two packages respectively. As shown in Fig. (3), a metatarsal bone model was constructed by extruding the x-y profile of Fig. (1) normal to the profile plane. This model is only a rough approximation of the real bone, but it greatly simplifies analysis and interpretation. This simplification is justified because forces acting on the bone lie almost entirely in the sagittal plane, and bone movement is restricted to this plane only. Using a more realistic 3-D bone model would not add significant correction to the 2-D model; consequently, we chose to use the 2-D model, in order to reduce complexity and time-consuming computation.
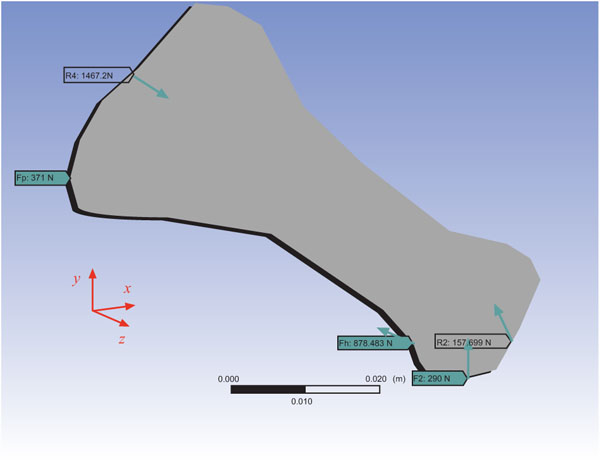
Forces on the metatarsal bone model used for Finite Element Analysis. Values are calculated, based on Reference 6 (Jacob, Clin Biomed, 2001), assuming a body weight of 100 kg.
Anthropometric data and forces (Fig. 3) were taken from the 2001 Jacob study [6] where all the forces are expressed in % body weight, which was set arbitrarily to 100 kg for this analysis (forces on the joints had to be slightly rotated in order to get equilibrium conditions). Table 1 contains the x-y force components in Newtons. More specifically, F2 is the external ground force, Fh equals Fhl + Fhb where Fhl and Fhb are the forces acting along the tendons of the flexor hallucic longus and flexor hallucic brevis muscles respectively; Fpl is the xy-component of the peroneus longus force, and R4 and R2 are equilibrium forces on the tarsometatarsal and metatarsophalangeal joints from the neighboring bones. In order to calculate the maximum stresses on the cuts, the bone is drawn with a 350 angle to the floor (Fig. 1), which is the angle the bone takes [4] during the push-off phase (second force peak during stance).
Forces (in Newtons) at the Metatarsal Bone Model Presented in Fig. (3)
| Symbol | x-Value | y-Value | Origin |
|---|---|---|---|
| F2 | 0 | 290 | External ground force |
| Fhl | -475 | 221 | Flexor hallucis longus muscle |
| Fhb | -329 | 133 | Flexor hallucis brevis muscle |
| Fpl | -371 | 0 | Peroneus longus force |
| R2 | -62.1 | 145 | Tarsometatarsal joint |
| R4 | 1237 | -789 | Metatarsophalangeal joint |
The ANSYS bone model was divided in 14000 elements in total, with 8300 nodes on the xy plane, whereas the OOF bone model was divided in 8000 elements with 8000 nodes on the xy plane. Bone dimensions were 66 × 37 × 10mm and bone volume was 12.8 cm3. The following bone material constants were used [9]: Elastic modulus 20 GPa, Poisson’s ratio 0.3, density 1.94g/cm3 (average values). Calculated bone mass was 24.3 g.
RESULTS
Followup data from clinical application of this new method were collected an average 32.7 months after the operation (Table 2). Mean preoperative HVA was 34.1 degrees (range, 22 to 56 degrees) and mean preoperative IMA was 15.5 degrees (range, 10 to 29 degrees). At the last follow-up examination, mean postoperative HVA angle was 14.2 degrees (range, 0 to 28 degrees), mean postoperative IMA angle was 8.1 degrees (range, 6 to 22 degrees), and mean AOFAS score was 94.3 (range 67 to 100). Results were rated as excellent in fifty feet (80.64%), good in 8 feet (12.9%) and fair in 4 feet (6.45%). All osteotomies were fused and there were no cases of non-union, loosening, avascular metatarsal head necrosis or wound infection. Two patients with fair results experienced late recurrence of the deformity, but this was not clinically significant, and they refused any further treatment.
Results of the Modified Chevron Osteotomy and Herbert Screw Fixation at Follow-Up (Mean Follow-Up Time 32.7 Months, Range 24-54 Months)
* At time of operation.
† Numbers in parentheses indicate ranges.
Both software packages (ANSYS and OOF) performed linear static structural FEA calculations and their outputs consist of sets of stress vector components along specific coordinate axes on each node of the model. Both data sets can be found as supplementary info at the web links listed in the Appendix [16, 17]. From these values, the average normal and average shear stress was calculated on the nodes of the 600 and the 900 osteotomies (Figs. 4, 5). In general, normal compressive (positive) stresses along an interface tend to keep the two parts together, while shear stresses tend to slide the two parts apart. Therefore better bonding is expected where the normal-to-shear stress ratio λ is positive and greater than 1. Table 3 shows the average λ produced by the two methods along the segments AC, CA’, BC and CB’ (Fig. 1) of the two osteotomies. For ease of comparison, all ratios are normalized in the 0 to 1 range. In general, FEA methods are complex and their results include some degree of uncertainty; however, in the present work we only attempted qualitative analysis, with no emphasis on detailed numerical data. In this qualitative fashion, results obtained with the ANSYS and OOF methods agree reasonably well. In particular, both methods predict that the largest λ occurs along the CA segment of the ACA’ (Fig. 1) osteotomy and it is 2 to 3 times larger than the second largest λ which occurs along the CB’ segment of the BCB’ osteotomy. Therefore a stronger bonding is expected for the 900 ACA’ osteotomy compared to the classical 600 Chevron osteotomy BCB’, and this finding may explain our excellent clinical results. However, the CA’ and the BC segments should also be taken into account, and both methods predict low normal stresses on these segments (Table 3). These interfaces will also influence healing time, but we believe that the strong bonding of the CA segment is the prevailing factor.
Normalized Normal-to-Shear Stress Ratio Calculated by the Two FEA Packages for the Two Osteotomies of Fig. (1)
| Section | ANSYS | OOF |
|---|---|---|
| AC | 1.00 | 1.00 |
| CA | 0.20 | 0.08 |
| BC | 0.32 | 0.03 |
| CB | 0.35 | 0.47 |
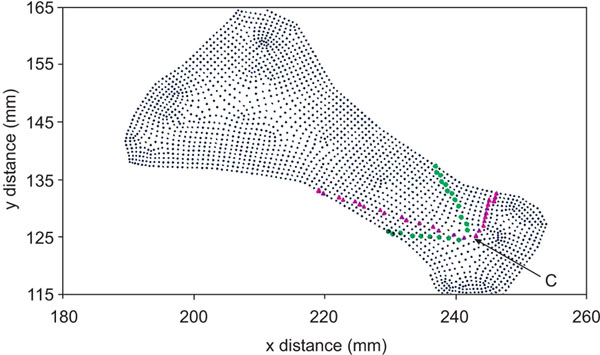
A plane x-y view of the bone model shown in Fig. (3), with Finite Element Analysis nodes (tiny dots) created by the ANSYS software while evaluating normal and shear stresses with the 60o and 90o osteotomies. Due to the discrete nature of the analysis, the two osteotomies cannot be represented by exact straight segments. Filled triangles indicate the nodes chosen to represent the 900 osteotomy, whereas filled circles indicate the nodes chosen to represent the 600 osteotomy. Point C (arrow) is the center of the circle shown in Fig. (1).
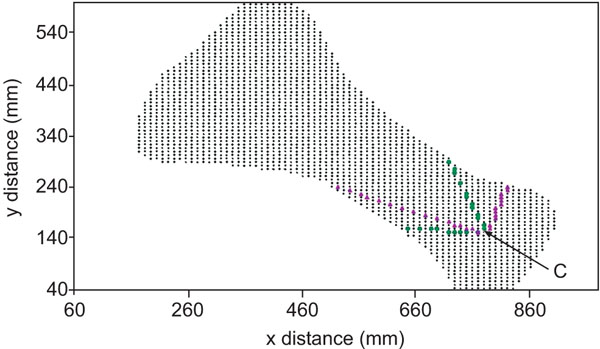
A plane x-y view of the bone model shown in Fig. (3), with Finite Element Analysis nodes (tiny dots) created by the OOF software while evaluating normal and shear stresses with the 60o and 90o osteotomies. Due to the discrete nature of the analysis, the two osteotomies cannot be represented by exact straight segments. Filled triangles indicate the nodes chosen to represent the 900 osteotomy, whereas filled circles indicate the nodes chosen to represent the 600osteotomy. Point C (arrow) is the center of the circle shown in Fig. (1).
DISCUSSION
Our results indicate that the 900 angle may be a good choice for Chevron osteotomy. Good clinical results have been reported in 80-90% of patients having the typical 600 osteotomy [4, 6, 9] with recurrences or under-corrections occurring in 10-14% of cases [5, 7, 8]. However, a recent study by Torkki et al. [10] reported inferior results, probably due to the number of different surgeons (including trainees) who performed these operations and the unselected study population.
Data obtained from applying FEA analysis to a bone model seem to explain the good clinical results observed in our patient cohort. These results are easier to explain physically if the bone is approximated by a straight long beam under longitudinal compression. This is a well known example in the theory of elasticity, with maximum and zero normal stress along the directions of 00 and ± 900 with respect to the beam axis, and maximum shear stress at ± 450. In the case of the metatarsal bone, all forces in Fig. (3) (except F2) are almost parallel to the long axis of the bone. Because the metatarsal bone has an elongated shape, this bone can be approximated by a beam, and this crude approximation can help us understand the distribution of stresses along the bone. As the ± 300 BCB’ osteotomy (Fig. 1) is close to the ± 450 case, a large shear stress is to be expected. In contrast, as the AC and CA segments resemble the 900 and 00 cases, normal stresses are expected to be maximum and zero respectively.
CONCLUSION
In this manuscript we present our experience with the 90-degree Chevron osteotomy on a patient cohort of 51 women who had surgery for 62 Hallux Valgus deformities, and we also present results of Finite Element Analysis (FEA) of the 90o Chevron osteotomy. Compared to the 60o method, FEA predicts enhanced mechanical bonding, with stronger compressive stresses and weaker shearing stresses with the 900 Chevron osteotomy. Our good long-term clinical results, together with results of Finite Element Analysis, suggest that the 900 angle Chevron osteotomy is a good alternative to the classic 60o method in patients with mild to moderate Hallux Valgus who need surgery.
AUTHOR CONTRIBUTIONS
Charalambos Matzaroglou, performed many operations, collected data and drafted manuscript.
Panagiotis Bougas, assisted with most operations and collected data.
Elias Panagiotopoulos, supervised most operations, directed patient care and revised manuscript.
Alkis Saridis performed many operations, collected data and revised manuscript.
Menelaos Karanikolas provided anesthesia for many procedures, organized, revised and submitted manuscript.
Dimitris Kouzoudis provided data, conducted Finite Element Analysis, and revised manuscript.
CONFLICT OF INTEREST
This work was supported solely by Department Funds. All authors declare that they have no conflict of interest to report.
ACKNOWLEDGEMENTS
The authors would like to thank Vassilis Stefanidis, University of Macedonia, Greece, for his invaluable assistance on installing and configuring the OOF2 package on a Linux system.
APPENDIX
The outputs of two packages ANSYS and OOF consist of sets of stress vector components along specific coordinate axes which can be found at the web links
http://www.ephysics.des.upatras.gr/chevron90fea/ansysExport.xls
and
http://www.ephysics.des.upatras.gr/chevron90fea/oofExport.xls


