All published articles of this journal are available on ScienceDirect.
Osteochondral Grafting: Effect of Graft Alignment, Material Properties, and Articular Geometry
Abstract
Osteochondral grafting for cartilage lesions is an attractive surgical procedure; however, the clinical results have not always been successful. Surgical recommendations differ with respect to donor site and graft placement technique. No clear biomechanical analysis of these surgical options has been reported. We hypothesized that differences in graft placement, graft biomechanical properties, and graft topography affect cartilage stresses and strains. A finite element model of articular cartilage and meniscus in a normal knee was constructed. The model was used to analyze the magnitude and the distribution of contact stresses, von Mises stresses, and compressive strains in the intact knee, after creation of an 8-mm diameter osteochondral defect, and after osteochondral grafting of the defect. The effects of graft placement, articular surface topography, and biomechanical properties were evaluated. The osteochondral defect generated minimal changes in peak contact stress (3.6 MPa) relative to the intact condition (3.4 MPa) but significantly increased peak von Mises stress (by 110%) and peak compressive strain (by 63%). A perfectly matched graft restored stresses and strains to near intact conditions. Leaving the graft proud by 0.5 mm generated the greatest increase in local stresses (peak contact stresses = 6.7 MPa). Reducing graft stiffness and curvature of articular surface had lesser effects on local stresses. Graft alignment, graft biomechanical properties, and graft topography all affected cartilage stresses and strains. Contact stresses, von Mises stresses, and compressive strains are biomechanical markers for potential tissue damage and cell death. Leaving the graft proud tends to jeopardize the graft by increasing the stresses and strains on the graft. From a biomechanical perspective, the ideal surgical procedure is a perfectly aligned graft with reasonably matched articular cartilage surface from a lower load-bearing region of the knee.
INTRODUCTION
Chondral lesions are more prevalent than previously believed. Full-thickness lesions are found in approximately 20% of knee arthroscopies and are located most commonly in the medial femoral condyle [1-4]. Even partial-thickness asymptomatic cartilage defects can progress within a 2-year period resulting in the reduction in cartilage volume [5].
Various treatment options are recommended for full-thickness chondral and osteochondral lesions, although consistent long-term clinical results are not yet available [6]. Surgical options can be classified into repair (microfracture and abrasion arthroplasty), regeneration (ACI), and replacement (osteochondral grafting) [7]. When repair results in tissue that is typically fibrocartilaginous, replacement often produces cartilage that is hyaline in nature. However, several weeks are required for the injected cells to regenerate tissue and clinical recovery is slower than with osteochondral grafting [8]. Osteochondral grafting is currently the only surgical procedure that immediately replaces the lesion with native hyaline articular cartilage [9].
Several types of surgical instrumentation are available and various surgical options are recommended. One option is to create the recipient hole at a depth 2 mm less than that of the donor graft height rather than to match recipient depth with graft height [6]. Another option is to align the graft articular surface flush with the surrounding cartilage [6]. On the other hand, grafts that are countersunk or recessed slightly below the surrounding articular surface tend to thicken and remodel to restore articular surface congruity [10]. Yet others have speculated that a proud graft could settle to an optimum level with weight bearing [11]. One finite element analysis, using idealized axisymmetric geometry, indicated that graft–recipient height mismatch altered joint stresses [12]. An in vitro study of 4.5-mm osteochondral defects in swine knees also reported elevated peak contact pressure with graft–recipient misalignment [13]. However, no clear biomechanical analysis has been performed on the effect of graft placement, material properties, and curvature under clinically relevant geometry and in the presence of an intact meniscus.
The finite element method was therefore used to study the effect of differences in graft placement, graft biomechanical properties, and graft topography on cartilage stresses and strains at the site of the cartilage lesion. We chose the medial femoral condyle because of the propensity for a full-thickness chondral lesion [2]. We studied an 8-mm diameter defect because it was within the range of cartilage defect sizes reported during arthroscopy, was large enough for treatment to be indicated, and was small enough to require a single osteochondral graft [1, 14-16].
METHODS
Geometry
MRI scans were obtained from a young adult male knee that was scanned with three-dimensional spoiled gradient echo (slice thickness = 1.5 mm). The articular surface of the femur, tibia, and meniscus was extracted by image segmentation using a commercially available software program (MIMICS, Materialise, Leuven, Belgium). For this study, the articular cartilage of the medial compartment and medial meniscus was meshed at a constant thickness of 2 mm with hexahedral elements using Hypermesh (Altair Engineering, Irvine, CA) [17]. The mesh density selected resulted in an average element size of 0.5 mm x 0.5 mm x 0.5 mm (Fig. 1).
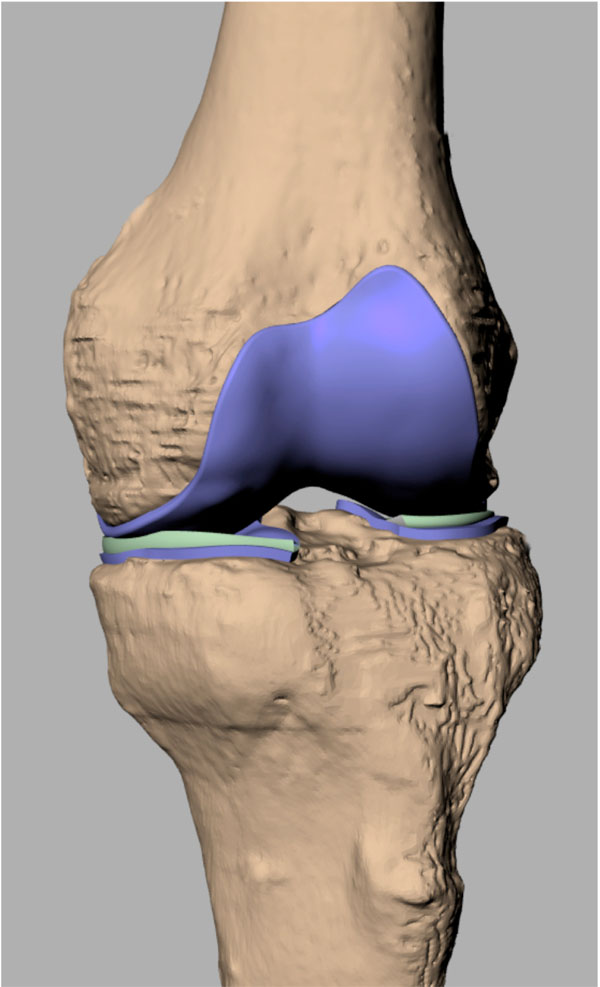
The finite element model of femoral and tibial articular cartilage and the menisci. The geometry was reconstructed from a MRI of an adult male knee.
Material Properties
Articular cartilage was modeled as a linear elastic material (Young’s modulus = 15 MPa, poisson ratio = 0.45). Loading rates during walking are too rapid to permit significant fluid flow; therefore, articular cartilage can be treated as a linear elastic material. The meniscus was modeled as a transversely isotropic material with E1 = E2 = 20 MPa in the vertical and radial directions; E3 = 150 MPa in the circumferential directions; the in-plane poisson ratio = 0.2, the out-of-plane poisson ratio = 0.3, and shear modulus = 57.7 MPa [18].
Boundary Conditions
The bottom nodes of the articular cartilage mesh were tied to rigid surfaces representing the subchondral bone of the femur and the tibia. Initial simulations with the subchondral bone modeled with stiffness of the cortical bone (20 GPa) resulted no significant differences in the contact stresses, which has also been previously reported [19]. Using rigid bodies reduced the computational time for the high-density cartilage mesh necessary to achieve convergence in graft contact outcomes. Nodes at the anterior and posterior horns of the medial meniscus were also attached to the tibial subchondral springs with linear springs (net stiffness for each horn = 2000N/mm) [19]. The tibia was constrained in the mediolateral and the anteroposterior directions but was allowed to translate superiorly under a compressive load of 350N. The femur was constrained in the superoinferior direction but was allowed to translate in the mediolateral and the anteroposterior directions. This reproduced the loading conditions in a human cadaver study of osteochondral defects, the results of which were used for model validation [20]. Global frictionless contact was modeled between the femoral and tibial cartilage, between the femoral and meniscal articular surfaces, between the tibial and meniscal articular surfaces, between the graft and tibial articular surfaces, and between the sides of the graft and recipient cartilage.
Explicit Analysis
After the femoral and tibial surfaces were brought into contact, the compressive load of 350N was applied over 1 second (Fig. 1). An explicit solver (Abaqus 6.7, Dassault Systèmes, Simulia, Providence, RI) was used to solve the quasi-static analysis.
Study Conditions
The following conditions were simulated: an intact femoral condyle with and without a meniscus, a defect 8 mm in diameter, and a defect filled with a graft 8 mm in diameter. The graft position was varied at 0.25 mm increments such that the graft was either recessed below or proud above the surface of the surrounding recipient area. The elastic modulus of the graft either matched the modulus of the recipient cartilage, was decreased by 33%, or was increased by 33% to simulate the varying modulus reported for articular cartilage at different locations in the knee [21]. The topography of the graft was also varied since the topography of surface of the femoral articular cartilage varies significantly based on location. The curvature at the site of grafting for this knee was 23 and 42 m-1 in the anteroposterior and mediolateral directions, respectively; very close to the reported mean for the medial femoral condyle [17]. Based on the mean values reported for typical donor sites in the trochlea and the femoral condyle, we varied the curvature of the graft surface between 5 m-1 (minimum curvature of proximal medial trochlea) and 70m-1 (maximum curvature of lateral trochlea).
RESULTS
Peak contact stresses were 3.4 MPa for the intact condition and increased slightly to 3.6 MPa in the presence of an 8-mm osteochondral defect (Fig. 2). On the other hand, peak von Mises stresses and peak principal strain increased more dramatically by 110% and 63% in the presence of an osteochondral defect. In the absence of the meniscus, the contact stresses increased more substantially to a peak of 5 MPa.
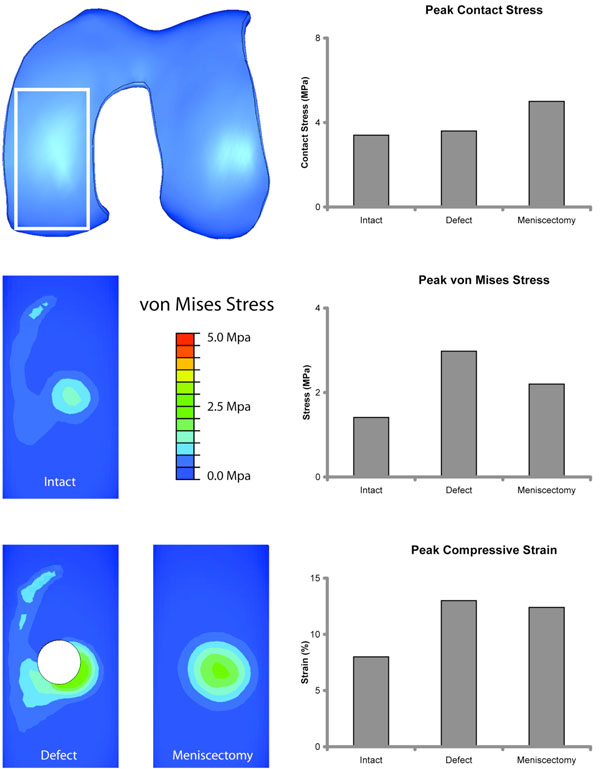
Analysis of Intact, Defect, and Meniscectomy Conditions. Inferior view of medial femoral condyle cropped to the white rectangle. Left column: Contour maps of von Mises stress distribution for the Intact condition, Defect, and Meniscectomy conditions. Right column: Peak contact stresses, von Mises stresses, and compressive strains are charted. While peak contact stress did not increase significantly in the presence of a defect, peak von Mises stress and compressive strain were substantially elevated.
As expected, replacing the osteochondral defect with a perfectly matched graft restored peak contact stresses, von Mises stresses, and compressive strains to levels very close to those seen in the intact condition (Fig. 3). Leaving the graft proud by as little as 0.25 mm significantly increased peak contact stresses, von Mises stresses, and compressive strains in the graft but reduced these measures (except for compressive strains) in the recipient area surrounding the graft. Recessing the graft tended to have the converse effect with reduction of peak contact and von Mises stresses in the graft and an increase in the adjacent recipient contact area.
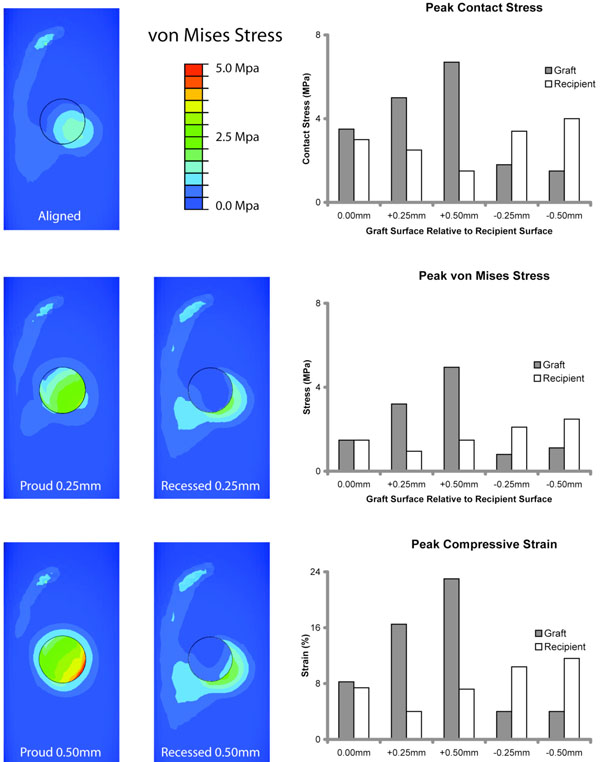
Analysis of Graft surface alignment. Left column: Contour maps of von Mises stress distribution for various alignment conditions showing significant increase with proud placement of the graft. Right column: Leaving the graft proud significantly increased peak contact stresses, von Mises stresses, and compressive strains in the graft. Recessing the graft tended to reduce of peak contact and von Mises stresses in the graft (‘+’ indicates a graft raised above the recipient surface, ‘-‘ indicates a graft recessed below the recipient surface).
The material properties of articular cartilage vary based on the location within the joint. The typical donor sites (lateral margin of the trochlear groove, posterior femoral condyles, anteromedial margin of the medial femoral condyle, anterolateral portion of the intercondylar notch) have a lower elastic modulus. We therefore varied the elastic modulus of the graft by ±33%. A near linear correlation between graft stiffness and peak graft contact and von Mises stresses was found (Fig. 4).
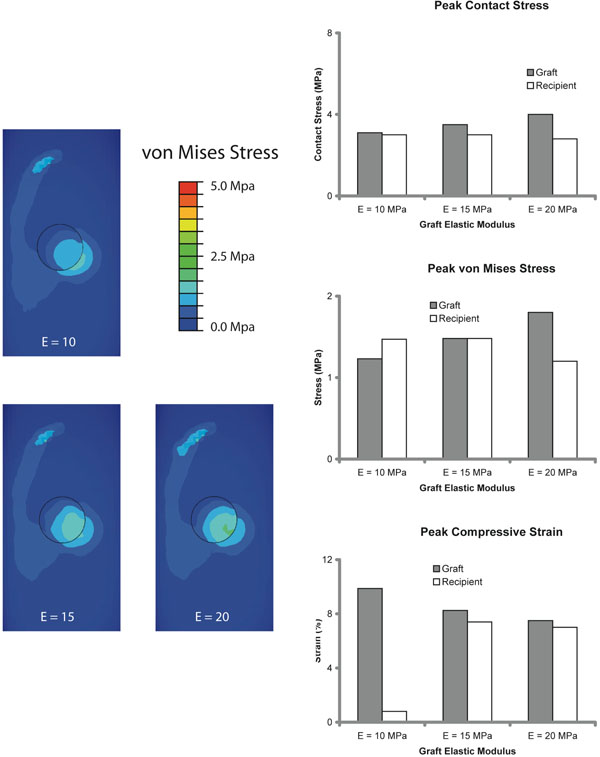
Results of Variation in Graft Modulus. Left column: Contour maps of von Mises stress distribution for grafts of different stiffness (E = Young’s modulus). Right column: Graft stresses linearly increased with graft stiffness.
We varied the curvature of the articular surface of the graft to represent the least curvature of a graft harvested from the proximal medial trochlear region (5m-1) and the maximum curvature of lateral trochlea (70m-1); two sites that are commonly recommended as donor sites. Changing graft curvature generated a moderate increase in peak contact stresses, von Mises stresses, and compressive strain (Fig. 5). Increasing the graft curvature had a greater effect than decreasing the graft curvature.
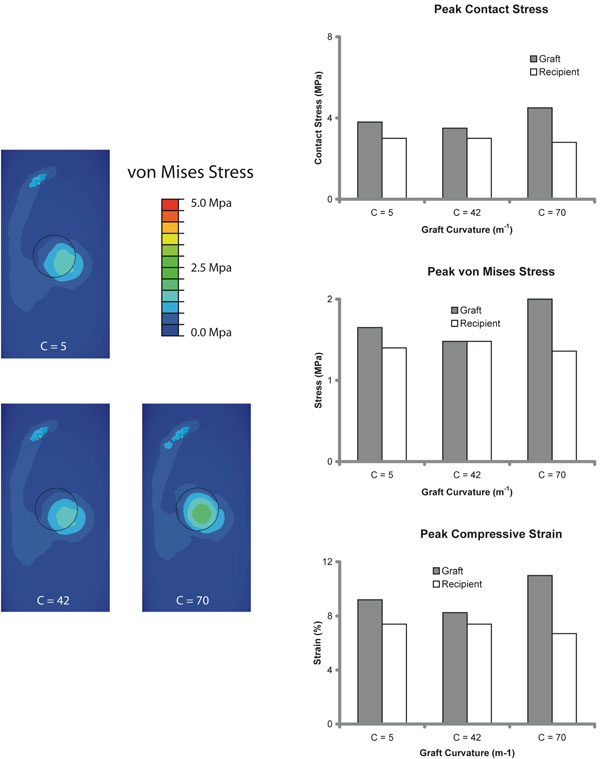
Results of Variation in Graft Curvature. Left column: Contour maps of von Mises stress distribution show the location of peak stresses for grafts of different curvature (C = graft curvature). Right column: Increasing the graft curvature increased stresses and strains.
DISCUSSION
We designed the study to analyze the stresses and the strains generated in the graft and the recipient area under conditions simulating normal walking. We determined the sensitivity to surgical parameters, such as graft alignment, and to recipient parameters, such as articular surface curvature and biomechanical properties of the donor region. The objective was to improve surgical technique by determining the optimum mechanical conditions for graft survival and integration.
Contact stresses generated by the finite element analysis in the intact 8-mm defect and by the meniscectomy condition were validated against published experimental reports. The peak contact stress (3.4 MPa) in the intact femoral condyle at 350N compressive load was close to the experimentally measured mean in human cadaver knees (~3.5 ± 1.5 MPa) under similar loading conditions [20]. Peak contact stress increased slightly (to 3.6 MPa) around the rim of the 8-mm diameter defect. Experimentally, no significant change in peak contact stress was reported for defects of this size [20].
There is some debate over the relationship between the defect size and the increased contact stresses. It has been theorized that contact stresses should increase around a defect. Experiments have also shown an increase in contact stresses around larger defects (16 mm in diameter) [22]. On the other hand, it has been shown that peak contact stresses may be unchanged in the presence of small cartilage defects [20, 23]. In the intact condition, the curved femoral condyle on a relatively flat tibial plateau concentrates contact near the centroid of the contact patch. In the presence of a defect, the contact area tends to increase and is distributed centripetally around the margins of the defect thus reducing contact stresses. Additionally, in a defect a greater proportion of the tibiofemoral load is transmitted through the meniscus away from the central tibiofemoral contact. In our model, meniscectomy increased peak contact stress by 43%, which was well within experimentally measured peak tibiofemoral contact stresses after medial meniscectomy in human cadavers (Range, 18%-235%) [24-26].
Contact stresses are an important factor for surface wear but may not directly relate to subsurface stresses. Contact stresses have received more attention in part because measuring contract stresses is experimentally more feasible than measuring subsurface stresses. While contact stresses have been used as a marker for wear in artificial materials and may be somewhat related to cartilage damage, the subsurface stresses are likely to be more important in determining potential for cell death in the deeper layers, delamination and fragmentation of cartilage, and debonding from subchondral bone, which is often observed during arthroscopy. In direct contrast to the slight increase in contact stresses, the osteochondral defect generated a substantially greater increase in peak von Mises stresses (a more common measure of material yielding [27]) and peak compressive strain, which has been shown to be related to chondrocyte injury [28]. Further, the peak compressive strains were located at the margins of the defect at the junction with subchondral bone, indicating a potential site for initiation of progressive cartilage damage. These results provide biomechanical support for the clinical report of progression of asymptomatic cartilage defects within a 2-year period [5].
Grafting restored peak contact stress, von Mises stress, and compressive strain to near intact levels. This has been shown in previous studies [13, 22]. However, graft-surface alignment had a significant effect on these measures consistent with the increase in contact pressure reported in an experimental study on swine knees [13]. When the graft was kept proud, the peak contact stress, the von Mises stress, and the compressive stain in the graft increased significantly. Although recessing the graft reduced these stresses and strains, a substantial increase was noted in the recipient area surrounding the graft. Of all the conditions tested (meniscectomy, graft alignment, graft material property, graft curvature) keeping the graft proud by 0.5 mm generated the greatest increase in stresses and strains. Even a 0.25 mm increase in graft surface over recipient surface height generated higher stresses. The peak contact stress and peak compressive strain approached levels that have been shown to induce cartilage damage and cell death [28-32]. A freshly harvested graft may be even more susceptible to damage. Note that our model does not account for graft subsidence due to collapse and compaction of the donor bone, which may occur in vivo.
Two important biomechanical factors, which can vary significantly between the donor area and the recipient site, are the material properties of the cartilage and the curvature of the articular surface [17, 21]. We varied the elastic modulus of the graft by ±33% relative to the recipient site and noted a general increase in contact and von Mises stresses in the graft with increasing elastic modulus. The peak compressive strain however decreased with increasing modulus, because the softer graft compressed more under otherwise identical conditions. Lower graft modulus is a clinically more relevant condition, since the donor sites are typically harvested from low load-bearing regions. Overall, reducing graft modulus did not generate detrimental stresses and strains. Altering graft curvature within the range reported for typical donor sites also produced modest changes in the stresses and strains. In general, a graft with a lower curvature, such as the proximal medial trochlea, was more forgiving than a graft with a greater curvature. This biomechanical analysis supports the use of commonly recommended donor sites despite the variations in modulus and topography.
One weakness of our model was the use of single-subject geometry. This is a common weakness of computer models, and almost all finite element models of the articular cartilage and meniscus have used a single geometry [19, 23, 33, 34]. Condylar shape and meniscal geometry can affect stress magnitudes and distribution. However, the between-subject variability is high [20] and requires a larger sample size to obtain statistically significant differences. While the precise magnitudes of stress and strain may vary among knees, the trends reported in our study will likely be applicable to other knee geometries and the close approximation with experimentally reported average results validates our model [20]. Donor thickness may also affect stresses, but donor and recipient thicknesses do not vary significantly [17]. Other weaknesses include using a single-defect location and using a single-sized graft. Finally, we did not study biological factors, which may be more important in graft–recipient healing.
An osteochondral defect did not result in substantially increased contact stresses, but other biomechanical markers of potential for tissue damage and cell death, such as von Mises stresses and compressive strain, were markedly increased. Leaving a graft proud tends to jeopardize the graft by increasing the potentially deleterious stresses and strains on the graft. Recessing the graft transfers the stresses to the adjacent recipient area. Reducing the elastic modulus of the graft by up to a third did not significantly affect stresses or strains. Donor–recipient mismatch in articular surface topography also modestly increased stresses and strains. From a purely biomechanical perspective, the ideal surgical procedure is a perfectly aligned graft with reasonably matched articular cartilage surface from a lower load-bearing region of the knee.
ACKNOWLEDGEMENTS
This study was funded by Scripps Health Foundation philanthropic funds.


